G. V. Hoppa and B. R. Tufts, LPL, University of Arizona, Tucson, AZ 85721-0092 (hoppa@lpl.arizona.edu).
 
 

Introduction: The formation of cycloidal ridges on Europa has been a mystery dating back to the Voyager encounter [1,2]. Fig. 1 shows examples of cycloidal ridges viewed by the Voyager spacecraft. In addition, widespread arcuate tectonic features (including for example the dark wedge shaped bands) are unexplained. Previous models for the formation of cycloidal and other arcuate features depended on compression and thrust faulting [2,3] which could be analogous to island arcs on the Earth [4]. High-resolution Galileo images have revealed that cycloidal ridges are in fact double ridges (Class 1 in the Greenberg et al. taxonomy [5]). Additional Galileo images reveal cycloidal cracks without ridges and/or with tectonic displacement subsequent to initial cracking. Here we propose a model for the formation of arcuate features as tension cracks due to diurnal tidal stress.

Figure 1

Diurnal Tidal Stress: As Europa orbits Jupiter, the amplitude and orientation of its tidal bulge varies with an 85 hour period. Resulting diurnal tides due to Europa's orbital eccentricity may be a significant source of stress on Europa's ice shell. Global tidal stress models have been developed to explain the formation and global patterns of linear features on Europa [3,5,6,7,8]. To explain the formation of cycloidal features we use the Greenberg et al. [5] diurnal stress calculations. This model assumes a thin ice shell on top of a global ocean which experiences a ~30 meter change in tidal amplitude over 42.5 hours. The magnitude of the tidal stress is proportional to m(1+n)/(5+n) where m is the shear modulus and n is the Poisson ratio. Values of m=9.2x10⁹ Pa and n=0.33 [9] were adopted. This model gives the stress field for any location on Europa at any point during its orbit.

Forming Cycloidal Features: Cycloidal features may be formed as tensile cracks responding to Europa's tides. When the tensile strength of ice is reached a crack begins to form perpendicular to the local direction of the tensile stress. Because diurnal tidal stress changes, cracks propagate across an ever changing stress field (in both amplitude and orientation). Thus, propagation can follow a curving path until it reaches a place and time where the tensile stress is insufficient to continue the propagation. The propagation may be dormant until a few hours later when the stress at the end of the crack once again exceeds the strength and propagation continues (usually at a different orientation than when the crack propagation stopped), A cusp forms because the orientation of the tidal stress field has significantly changed during the period that the crack was inactive.

In addition to the diurnal stress model [5], three additional parameters are required to model cycloidal features: a) the amplitude of the stress field required to initiate cracking, b) the amplitude of the stress field where cracking halts, and c) the horizontal crack propagation velocity. The maximum diurnal tensile stress is ~1 bar, however, most regions are not stressed so much. Considering that cycloidal features have been observed at numerous locations on Europa, we assume that crack initiation begins at 0.7 bar, which would allow these features to form at many latitudes and longitudes. Once the crack begins to form we assume that less stress is required for it to continue to propagate. Crack propagation continues until the tensile stress drops below a minimum value (we assume 0.4 bars). Finally, if the horizontal crack propagation is slow, e.g. at a few km per hour, it follows the orientation of the rotating diurnal stress field. This velocity is also consistent with forming cusps spaced between 75-150 km. Variations in the parameters to initiate and stop cracking (~0.1 bar), and variations in the crack velocity need to be invoked to model observered cycloidal features at different orientations and locations.

Cycloidal features are modeled by the following steps. The diurnal stress field is calculated at a selected point on the surface. When the tensile stress reaches 0.7 bar, crack initiation begins in the direction perpendicular to the orientation of the tensile stress. Once the crack is initiated we follow its propagation perpendicular to the local tensile stress. The curvature and length of each arcuate segment depends on the propagation speed; values between 2-4 km/hour (a slow walk) give geometries similar to those observed on Europa. We recalculate the stress field for each new position on the surface. As long as the tensile stress perpendicular to the crack remains above 0.4 bar the crack continues to form (Fig. 2). Eventually the stress drops below 0.4 bar, and the crack stops. Later crack propagation begins again once the tensile strength 0.7 bar is reached. Because a crack cannot propagate more than ~100 km per orbit, and because the diurnal stress field does not change dramatically over that distance, the next crack initiation begins approximately one orbital period after the initial propagation (Fig. 2). This forms the characteristic cusp associated with cycloidal features because the azimuthal orientation of the tension when the crack starts up again is nearly perpendicular to the orientation of the tension when the crack stopped on the previous orbit. Cycloids are formed over the successive orbits until the crack reaches a zone in the stress field where the tension never reaches the failure criteria or a geologic unit unfavorable for the crack to cross (i.e. chaos or active crack).

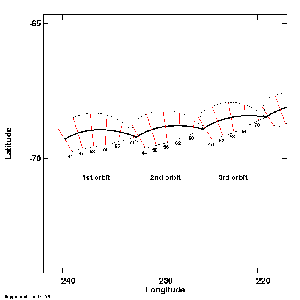Figure 2

Additional characteristics of cycloidal features may also be explained by this model. As shown in Fig. 1 some cycloidal features have cusps oriented upward (i.e. Delphi Flexus) right next to features with cusps oriented downward (i.e. Sidon Flexus). Our model explains the orientation of the cusps as a function of the direction of the crack propagation, as follows: features similar to Delphi Flexus (cusp upward) form when cracks propagate westward in the southern hemisphere, while features similar to Sidon (cusp downward) would form when cracks propagate eastward in the southern hemisphere. The opposite effect would take place in the northern hemisphere.

Most observed cycloidal features are skewed systematically (the radius of curvature varies along the length of the feature). We find that cycloidal cracks forming from diurnal tidal stress are similarly skewed if the crack propagation velocity varies as a function of the tension.

Discussion: This model provides a plausible explanation for the formation of cycloidal features on Europa as tensile cracks forming in response to the changing diurnal tidal stress field. This model can reproduce many of the major characteristics associated with cycloidal features including: a) the cycloidal segments, b) the cusps, c) the distances between cusps, d) the orientation of the cusps, e) the skewness along cycloids, f) the termination of cycloidal features, g) the overall curvature of these features. Cracks that are not cycloidal probably propagated faster. The presence of doublet cycloidal ridges (Class 1 in Greenberg et al. taxonomy [5]) suggest that ridge formation is a universal process (for cycloidal and non-cycloidal cracks) on Europa [5,10,11,12].

This model requires a global ocean close to the surface to generate significant tidal stress over a diurnal cycle. If indeed cycloidal features form in response to diurnal tides, then they form quickly over the course of a few days. Therefore, searches for changes on Europa [13] should look for evidence of new cycloidal cracks. The lack of these features on other icy satellites may indicate that only Europa has liquid water relatively close to the surface.

References: [1] Smith, B.A. et al. (1979) Science, 206, 927-950. [2] Lucchita, B.L., and L.A. Soderblom. (1982) Satellites of Jupiter, 521-555. [3] Helfenstein P., and M. Parmentier. (1983) Icarus, 53, 415-430. [4] Nolan, M., and R. Greenberg (1987) Bull. Am. Astron. Soc. 19, 860. [5] Greenberg, R. et al. (1998) Icarus, 135, 64-78. [6] Helfenstein P., and M. Parmentier. (1983) Icarus, 61, 175-184. [7] McEwen, A. (1986) Nature, 321, 49-51. [8] Leith A.C. and W.B. McKinnon (1996) Icarus, 120, 387-398. [9] Turcotte, D.L. and G. Schubert (1982) Geodynamics. Wiley, NY. [10] Head, J.W., et al. (1998) JGR-Planets, submitted. [11] Turtle, E.P. et al. (1998) Eos, 79, S202.. [12] Kadel, S.D., et al. (1998) LPSC XXIX, cd-rom. [13] Phillips, C.B., et al. (1998) LPSC XXIX, cd-rom.