*Lunar and Planetary Laboratory

University of Arizona

Tucson, AZ 85721
 
 

Send all correspondence to:

Gregory Hoppa

Lunar and Planetary Laboratory

University of Arizona

1629 E. University Blvd.

Tucson, AZ 85721-0092

Phone: 520-621-6520

Fax: 520-621-5133

email: hoppa@lpl.arizona.edu
 
 

17 pages

1 table

9 figures

Key words: Europa, Satellites of Jupiter, Rotation

Running Head: Rotation of Europa

Send all correspondence to:

Gregory Hoppa

Lunar and Planetary Laboratory

University of Arizona

1629 E. University Blvd.

Tucson, AZ 85721-0092

Phone: 520-621-6520

Fax: 520-621-5133

email: hoppa@lpl.arizona.edu
 
 

Abstract:

Tidal torques on Europa due to Jupiter would tend to drive Europa's rotation to a rate slightly faster than synchronous, unless synchroneity is maintained by a permanent asymmetry in Europa's mass distribution. Moreover, global fracture patterns on Europa's surface, as well as the complex fine-scale tectonics revealed by Galileo high-resolution imagery, may be evidence of stress due to non-synchronous rotation. A direct measurement of Europa's rotation rate is made from the positions of surface features relative to the terminator in a Galileo image and comparing the results with similar measurements of the positions of the same features relative to the terminator in a Voyager 2 image taken seventeen years earlier. Any non-synchronous rotation must be slower than a few tenths of a degree in 17 yr. (a complete rotation in >104 yr.) relative to the direction of Jupiter.
 
 

Key words: Europa, Satellites of Jupiter, Rotation

I. Introduction

Tidal torques due to Europa's eccentric orbit would tend to drive Europa's rotation to a rate slightly faster than Europa's orbital period. Thus, Europa's rotation must be non-synchronous unless synchroneity is maintained by a permanent asymmetry in Europa's mass distribution (Greenberg and Weidenschilling 1984). Europa's low and globally-distributed topography (£200 m elevation) (Smith et al. 1979, Belton et al. 1996) may not be capable of providing much asymmetry, and the possibility of a liquid water ocean beneath the icy surface would make a frozen-in elongation unlikely. Even if the silicate interior were locked into synchronous rotation, an ocean might allow the surface to decouple from the silicate interior permitting the ice shell to rotate at a different rate. Additionally, the global fracture patterns on the surface of Europa, as well as complex fine-scale tectonics revealed by Galileo high-resolution imagery, may be evidence of stress due to non-synchronous rotation (Helfenstein and Parmentier 1985, McEwen 1986, Geissler et al. 1998, Greenberg et al. 1998).

In this paper (Sec. II) we describe a technique for measuring Europa's rotation rate based on the position of the terminator in Voyager and Galileo images. In Sec. III we show the results of the rotation measurement and discuss the associated systematic and random errors. Sec. IV discusses constraints from additional measurements of Europa's terminator and limb and a comparison with rotation measurements of Io and Ganymede using a similar technique.

II. Measuring the rotation rate from the position of the terminator

The geometric terminator on a spherical planet is a great circle 90f from the sub-solar point. For a body without an atmosphere, the terminator marks a sharp boundary at sunrise and sunset. Regional topography can affect the position of the apparent terminator substantially. However, Voyager imaging (Smith et al. 1979) and Galileo imaging of Europa (Belton et al. 1996) have revealed a surface with low topography compared with lunar-sized bodies. On such a smooth surface, the geographic position of the terminator should be predictable given the ephemeris of Europa. Thus, a direct measurement of Europa's rotation rate (which would be a constant rate of 101.38 f/day for synchronous rotation) can be obtained by measuring the positions of surface features relative to the terminator as imaged by Galileo, and comparing the results with similar measurements of the positions of the same features relative to the terminator as imaged by Voyager 2 17 years earlier. In effect, the rotational positions of surface features are defined relative to the well-known direction of the sun.

Only one Galileo image (s0349875113) covers a region near the terminator that was similarly imaged by Voyager for comparison. It was taken at a resolution of 1.6 km/pixel during the spacecraft's first ("G1") orbit. A reprojected version (sinusoidal, equal area, with north up, and east to the right) is shown in Fig. 1 showing latitudes from 0f to 30f north, with selected reference features spanning longitudes 157f to 172f. By convention, longitudes are measured west of the prime meridian defined by the sub-Jupiter point. The corresponding image of the surface by Voyager 2 (c2065211) showing the same region at 1.6 km/pixel, with the terminator, is similarly reprojected in Fig. 2.

The marked features in Fig. 1 and Fig. 2 represent 25 features easily identifiable in both the Voyager and Galileo images. However, differences in viewing geometry and lighting may shift the apparent positions of features. For example, what seem to be only albedo features in the Voyager 2 image are found to be ridges in the Galileo image; the apparent position may be shifted by illumination and shadows. These problems are minimized by using the intersection points of lineaments as reference points and checking relationships to other local features to ensure that the same location was identified at the pixel-level for each reference point (Sec. III contains further discussion of precision). Approximately half of the reference features fall on Ino Linea and AutonoÎ Linea (see Fig. 2).

The apparent terminator in these images may be shifted from the actual position depending on the contrast stretch of the display (Fig. 3). In order to have an objective means of defining the observed terminator so as to be consistent between epochs, we analyze the brightness across the terminator (east-west pixel DN values) at latitude intervals corresponding to the pixel size. Examples of the many profiles across the terminator, from both the Galileo and Voyager 2, are shown in Fig. 4 and Fig. 5. The terminator longitude is objectively defined (at each latitude and for each epoch) by fitting straight lines separately to the flat night-side portion and to the sloping bright-side (which is nearly linear at these incidence angles for a Lambertian photometric function); the intersection of the straight lines is defined as the apparent terminator. Note that data within 40 km of the intersection are not used in the line fits, to avoid allowing local shadow effects at the terminator to skew the position.

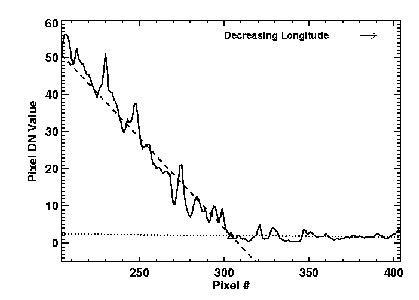Figure 4
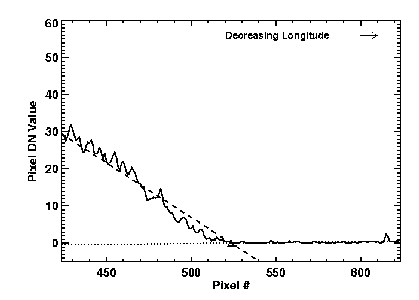Figure 5

The determination of the position of the apparent terminator was made over the full range of latitudes, generating the noisy terminator profile at the right in Fig. 1 and Fig. 2. The straighter curve through these points is a best-fit line (part of a great circle) parallel to the nominal terminator. The latter is not quite a north-south line, because the sub-solar latitude varies; it is at 1.39f N, 245.88f W for the Galileo image and 0.43f S, 231.75f W for the Voyager image. The twenty-five reference features were measured relative to the best fit line in both the Galileo and Voyager 2 image.

III. Results

For synchronous rotation between the Voyager and Galileo epochs, features in the Galileo image would be expected to be 14.13f closer to the terminator than in the Voyager image. In other words, if Europa were rotating synchronously, it would have rotated a whole number of times relative to the sun, plus 14.13f, in that time. The position of the terminator (relative to the surface features) in the Galileo image should be at the position of the dashed curve in Fig. 6, which is 14.13f to the left of its position in the Voyager image (Fig. 2). In fact, on average, the measured position of the terminator is only 13.0f from the Voyager position, suggesting slower-than-synchronous rotation by ~1f in seventeen years (0.059f/year).

This result would be contrary to the prediction by Greenberg and Weidenschilling in (1984): based on tidal torque, any non-synchronous rotation would be faster than synchronous. Before accepting the observation of slower-than-synchronous rotation, we must consider the precision of the measurements. Sources of random errors are (a) inconsistencies in measuring reference feature positions and (b) uncertainty in apparent terminator longitude.

Uncertainty (a) is due to the difficulty determining precise positions of reference features in the two images due to different photometric conditions, as discussed in Sec II. The reference features chosen could be identified to within a pixel in longitude in each image. The Galileo pixels are 1.6 km or 0.05f across, and the Voyager pixels are 1.8 km or 0.07f across. Thus feature location introduces an uncertainty of ±0.1f at most in our determination of rotation between the two epochs.

Uncertainty (b) comes from local topographic effects and noise in the images. In both images the position of the apparent terminator oscillates on either side of the best fit terminator (see Fig. 1 and Fig. 2). The standard deviation of the terminator longitude is ±0.4f for Voyager, and ±0.3f for Galileo. This variation is most likely due to random topographical features visible only at higher resolutions. Noise in the images from charged particles hitting the detector, especially in the Galileo image, could affect the slopes of the east-west reflectance profiles, thus altering the position of the apparent terminator at some longitudes. For this study we did not filter out charged particle noise, because it was important not to degrade geometric precision. Nevertheless the effect of noise is minimal because the best fit of the reflectance profiles averages over a large number of pixels. Random topography is the dominant cause of the deviation in terminator position.

The combined error from random sources (a) and (b) is ±0.5f, hardly enough to account for the 1.1f apparent shift due to non-synchronous rotation. Next we consider the sources of systematic error: (a) the shift in apparent position of the terminator in different geologic regions, (b) the effect of local topography, (c) the effect of Europa's global figure, and (d) photometric effects.

(a) The geological province may affect of the position of the terminator systematically. In the Voyager image the terminator crosses two different geologic provinces, the "brown mottled terrain" and "the bright plains", defined and mapped by Lucchitta and Soderblom (1982). Brown mottled terrain is a roughly textured, hummocky region of Europa, while the bright plains are identified by their high albedo. Fig. 7 shows the positions of the terminators viewed by Galileo and Voyager superimposed on the geologic map of Europa by Lucchitta and Soderblom (1982). The Galileo terminator lies primarily within the bright plains region. The Voyager terminator lies in brown mottled terrain except north of latitude 24f, where it crosses bright plains. In fact, we have found (Fig. 2) that the Voyager terminator is shifted (relative to the mean) to the east by 1f in the bright plains (north of 24f). Thus, when the calculation of Europa's rotation rate is limited to the comparison of terminator positions within the same geological province (the bright plains) rotation is found to be synchronous, with the uncertainty of ±0.5f.

(b) Local topography can also cause a systematic shift in the position of the terminator. On Europa, the shadow from a 100 m high ridge can reach the terminator from the day side 17.7 km (0.65f) away. From a 200 m ridge the shadow can reach the terminator from the day-side 25 km (0.92f) away. Such shadows preferentially shift the position of the apparent terminator in the direction of the sun. On the other hand, ridges on the dark-side of the terminator may be high enough to be illuminated by the sun. This would tend to move the terminator away from the sun, but this is less effective because the area of the illuminated ridge is much smaller than most of the region covered in darkness. Similarly, shadows from depressions tend to shift the position of the terminator in the direction of the sun. In order for these topographic effects to systematically affect this rotation experiment the character of the topography would need to different along the Galileo and the Voyager terminators. In fact there is a N-S ridge (Ino Linea) 32 km west of the terminator in the Galileo image. Such a ridge would have the potential for systematically shifting the terminator, however, we have avoided this source of error by not including the ridge or its shadow in the reflectance determination of the terminator (Sec. II). It is possible that the character of the topography varies between geological provinces so that the systematic shift discussed in (a) is due to local topography.

(c) The broad regional figure of Europa may also provide a systematic effect on the position of the terminator. Assuming an elliptical shape of for Europa due to a tidal bulge with an equilibrium amplitude of 500 m, the change in the position of the terminator with respect to the predicted location on a sphere would be negligible (<< 0.01f).

(d) Photometric effects could provide additional systematic effects on the position of the terminator. Dark albedo features would increase the slope of the reflectance curve and shift the terminator in the direction of the sun, while brighter features would have the opposite effect. This effect too may have contributed to the systematic effect due to the different geologic provinces (as above).

IV. Additional Constraints on Europa's Rotation Rate

A. Cilix

An independent determination of rotation was attempted by considering the position of the crater Cilix (1.7f N, 181.9f W) , which appears close to the terminator on a Galileo image taken on its third orbit. Figure 8 shows Cilix and the terminator of Europa as viewed by Voyager and Galileo. We can apply the same terminator-referenced comparison for these images as we did for Fig. 1 and Fig. 2. Unfortunately the Galileo image (s036839600) contains only 42 lines of data that cross the terminator. Also within this image, the rim of Cilix takes up 23 lines on top of the terminator. As discussed in Sec III, topography can have a systematic effect on the position of the terminator. Therefore we did not want to consider the portion of the image defined by the rim of Cilix. Additionally, Cilix is surrounded by an anomalously low albedo region that could also systematically shift the position of the terminator. Therefore out of the original 42 lines we can only use the top and bottom three lines to determine the position of the terminator. Comparing the position of this feature in both Voyager and Galileo images, we found a shift of 0.1f± 0.5f, consistent with synchronous rotation and similar to the results found in Sec. III.

B. Limb Fits

Other images permit another method of measurement of rotation. This method consists of fitting a limb or partial limb to an image of Europa in order to determine the precise latitude and longitude of features within the image. Galileo image s0383694600 from orbit E6 (1.5 km/pixel) and Voyager image c2064922 (1.9 km/pixel) have the appropriate geometry. As with the terminator images, a series of reference features (Fig. 9) were selected for comparison in both images. In this measurement all reference points are far from the terminator and thus are solely albedo features in both images. Therefore their positions are less ambiguous than before. Assuming synchronous rotation, the latitude and longitude of reference features in both images should be the same. The positions of features relative to the limb appear to be consistent with synchronous rotation (<0.1f±0.5f). Beam bending effects from the readout of the vidicon imaging system of Voyager may introduce uncertainties in the position of the limb by ±0.3f (Gaskell 1988). This measurement also relies heavily on the SPICE prediction data derived by JPL NASA to determine the precise locations of features on Europa. The software assumes that Europa is a sphere with a radius of 1561.5 km. In fact, however, Europa is a triaxial ellipsoid (a: 1563 ±1 km b: 1561 ±2 km c: 1559.5 ±1 km) (Thomas et al. 1997). This is not a serious problem because a 2 km uncertainty in the radius of Europa would translate to <0.1f error in position. Thus the shape of Europa is only a minor effect within this analysis.

V. Other Satellites

A. Io

Greenberg and Weidenschilling (1984) considered Io, like Europa, as a possible candidate for non-synchronous rotation, due to its forced eccentricity and high temperature. Unfortunately, the best high resolution images of Io's terminator by Voyager are near the south pole, not imaged by Galileo. However, the Galileo image s09413744178 (4 km/pixel), taken during orbit C10 and Voyager image c1639132 (500 m/pixel) show a common region with the terminator. The position of the terminator relative to identifiable features can be used to constrain the rotation rate just as we did for Europa.

Problems associated in this measurement include (a) surface changes due to Io's activity, (b) the large topography on Io, (c) great distance of the terminator from the reference features in the Galileo image, and (d) the low resolution of the Galileo image (4 km/pixel). We next consider each of these in turn:

(a) Io's volcanism can change the appearance of features over relatively short time scales. Active features have moved extensively over the seventeen years between Voyager and Galileo; Prometheus in particular has moved over 70 km (McEwen et al. 1998). The volcanic activity discourages the use of flows or low elevation features which may be easily altered over short time scales, but instead encourages the use of mountains that should be unchanged over long periods.

(b) Mountains on Io can drastically change the position of the apparent terminator. Carr et al. (1998) have identified mountains at least 7.6 km high on the surface of Io. These features could cast shadows up to 165 km in length (5f) across the surface. Within the Voyager image c1639132 a mountain shifts the position of the apparent terminator by ~2f. Therefore care was taken to avoid fitting a terminator in regions near known mountains.

(c) The terminator location in the Galileo image is separated from the Voyager image by 50f of longitude. As with the Europa images, the regional geology can also affect the position of the terminator. It is unreasonable to expect the character of the terminator to be the same over regions separated by ~1600 km, especially considering the topography of Io.

(d) The resolution of the Galileo image (4 km/pixel) also limits the constraints on Io's rotation rate. The lower resolution image limits the number of reference features that can be identified between the two images. This also limits the precision of the location of these features to within ±0.2f.

Taking all of these uncertainties into account, the comparison of the Galileo and Voyager images show that Io is rotating synchronously within 0.2f±1.5f.
 
 
 
 

B. Ganymede

Ganymede's rotation rate was also constrained using the terminator as a reference. Due to Ganymede's greater semimajor axis and smaller eccentricity, less torque is required to lock it into synchronous rotation (Greenberg and Weidenschilling 1984). The solid body of Ganymede could readily support a permanent asymmetry capable of locking the satellite into synchronous rotation. In fact, the topography of the large scale surface features may provide adequate asymmetry. Due to the limited number of images of Ganymede returned by Galileo, the only region in which this measurement could be made was at high northern latitudes (> 55f N). There, if non-synchronous rotation were occurring on Ganymede, any linear displacement of features would be approximately half of what would be observed near the equator. On Ganymede, eight features were measured with respect to the terminator in both a Voyager and Galileo image. These measurements indicate that Ganymede is rotating synchronously within 0.5f±1f.

VI. Discussion

We have found that the rotation of Europa relative to the direction of Jupiter is <0.5f over a 17 year period, i.e. one rotation with respect to Jupiter would require at least 12,000 years. Earlier, results from ground based photometric observations of Europa's disk-integrated lightcurve had shown that the darker hemisphere of Europa has remained on the trailing side over 50 years, constraining rotation to < 18f, i.e. a period > 1000 years (Morrison and Morrison 1977). Our new result is thus an improvement in the constraining of Europa's rotation rate by an order of magnitude and is consistent with synchronous, or very slowly non-synchronous, rotation.

Two lines of observational evidence suggest the rotation of Europa is in fact non-synchronous. Crater statistics on Europa do not reveal any leading-trailing asymmetry with an abundance of craters near the apex of Europa's leading hemisphere, such as would result from synchronous rotation (Shoemaker and Wolfe 1982). This is demonstrated by high resolution images (510 m/pixel) that sample the small crater population (Chapman et al. 1998), as well as global distributions of larger impact craters (>10 km) which appear to be randomly distributed (Shoemaker and Wolfe 1982). While the age of Europa's current surface is uncertain, between a few million and a billion years (Chapman et al. 1998), the lack of a leading-trailing cratering asymmetry is consistent with a non-synchronous rotation period much less than the age of the surface or more likely rapid resurfacing.

The other line of evidence suggesting non-synchronous rotation comes from apparent age sequences of linear features (Geissler et al. 1998). Cross-cutting relationships, revealed by multi-spectral imaging of the surface of Europa, show that the orientations of linear features rotate in the clockwise direction with age in the region around the intersection of the linear features Cadmus and Minos (45f N, 215f W). Maps of the tidal stress field due to non-synchronous rotation (Helfenstein and Parmentier 1985, McEwen 1986, Greenberg et al. 1998) show that, if the Cadmus-Minos region has moved from west to east over the last 60f of rotation, the local stress field would have rotated clockwise. This suggests that non-synchronous rotation may explain the age sequence in the Cadmus-Minos region.

Greenberg et al. (1998) have shown that the above explanation for the age sequence cannot be explained by the stress due to non-synchronous rotation alone. Although the clockwise rotation of local stress matches the trend observed in the cross-cutting geological relationships, the youngest linear features in the region would not form until some time in the future given the non-synchronous stress field. Greenberg et al. (1998) showed that the model is improved if "diurnal" tidal stress (due to the eccentric orbit) is added to the non-synchronous tidal stress. That result means that the non-synchronous stress cannot accumulate over more than ~1f of rotation, or else its magnitude would swamp out the diurnal stress. Moreover, it must accumulate for nearly that much rotation for the magnitude of the stress to crack the ice. The amount of stress accumulated may be limited either by the strength of the ice (it cracks before more stress accumulates) or by viscous relaxation (elastic stress can build only over limited time).

Consideration of the timescale for viscous relaxation leads to a lower limit on the non-synchronous rotation rate. Stress may begin to relax on short time scales in the warmer regions of the lithosphere. For a significant portion of the lithosphere (not including a superficial layer near the surface) , stress may build up for no more than ~100 years , based on the Maxwell time of ice at 200K. Thus Europa's rotation must be faster than 1f in 100 years (360f in 36,000 years) in order to produce enough stress. For the fastest possible rotation rate consistent with our terminator study (360f in 12,000 years), adequate non-synchronous stress is reached in 30 years (1f of rotation). Based on this line of argument, the rotation period appears to be constrained between 12,000 years (from our observations of the limb and terminator) and 36,000 years (from the relaxation time of the lithosphere).

There is, however, a problem with a period as short as 36,000 years. Since Cadmus and Minos formed <60f of rotation ago, that translates into ages of <6000 years. This is impossible because as triple bands they probably have developed mature ridges which likely form on time scales ?105 years (Greenberg et al. 1998). Thus based on the time scale for the possible formation of features it appears that the crust can support stresses for periods >100 years and that the non-synchronous rotation period must be at least 106 years.

Future missions to the Jovian system will provide additional constraints on the rotation rates of Europa and the other Galilean satellites. Voyager images may remain useful for these measurements because they have the advantage of being taken nearly 20 years ago which may compensate for their low resolution (~2 km/pixel). A few Galileo images taken at high resolution during the nominal mission include the terminator, but the advantage obtained through high resolution is diminished by the shorter time scale between Galileo and any foreseeable future mission. Table 1 sums up the best Voyager and Galileo images of the terminator that could be used in studies of Europa's rotation rate using future data. Many of the random and systematic uncertainties associated with determining the position of the terminator would remain however. If Europa's rotation rate is comparable to the upper limit allowed by our study, it should be detectable by appropriate images taken about 10 years from now, i.e. during the Europa orbiter mission currently being developed by NASA. If Galileo acquires an image of Europa's terminator at the equator at a resolution of 100 m/pixel, and if the future Europa orbiter obtains similar coverage, then the non-synchronous rotation rate can be constrained within 0.037f/10 years, (i.e. 360f in 105 years). Systematic errors due to regional geology would be reduced at higher resolution because the smaller field of view ensures that the terminators between the two images are within a few degrees of longitude. Similarly, if the resolution were 10m/pixel, the precision of would be proportionally better. Precise determination of the rotation rate of Europa could be measured with telemetry from a lander on the surface. Europa's rotation rate is probably a key determinant of its geological and geophysical evolution.

Acknowledgments:

We thank the technical staff of the Galileo project for making this study possible; the members of the Galileo imaging team, led by Mike Belton and their associates for their comments and suggestions; and C. Acton and N. Bachman at JPL for confirming geometric pointing information for the images used in this study. This work was funded in part by grant # 347050 from NASA's Planetary Geology and Geophysics program.
 
 

References:

Belton, M.J.S., J. W. Head III, A. P. Ingersoll, R. Greeley, A. S. McEwen, K. P. Klaasen, D. Senske, R. Pappalardo, G. Collins, A. R. Vasavada, R. Sullivan, D. Simonelli, P. Geissler, M. H. Carr, M. E. Davies, J. Veverka, P. J. Gierrasch, D. Banfield, M. Bell, C. R. Chapman, C. Anger, R. Greenberg, G. Neukum, C. B. Pilcher, R. F. Beebe, J. A. Burns, F. Fanale, W. Ip, T. V. Johnson, D. Morrisson, J. Moore, G. S. Orton, P. Thomas, R. A. West 1996. Galileo's first images of Jupiter and the Galilean satellites. Science, 274, 377-384.

Chapman C. R., W. J. Merline, B. Bierhaus, S. Brooks, and the Gailieo Imaging Team 1998. Cratering in the Jovian system: Intersatellite comparisons. LPSC XXIX, cd-rom.

Carr, M. H., A. S. McEwen, K. A. Howard, F. C. Chuang, P. Thomas, P. Schuster, J. Oberst, G. Neukum, G. Schubbert, and the Galileo Imaging Team 1998. Mountains and calderas on Io: Possible implications for lithosphere structure and magma generation. Icarus, 135, 146-165.

Gaskell, R. W. 1988. Digital identification of cartographic control points, Photogrammetric Engineering and Remote Sensing, 54, 723-727.

Geissler, P.E., R. Greenberg, G. Hoppa, P. Helfenstein, A. McEwen, R. Pappalardo, R. Tufts, M. Ockert-Bell, R. Sullivan, R. Greeley, M.J.S. Belton, T. Denk, B. Clark, J. Burns, J. Ververka, and the Galileo Imaging Team 1998a. Non-Synchronous rotation of Europa: Indications from Galileo observations. Nature, 391, 368-370.

Geissler, P.E., R. Greenberg, G. Hoppa, A. McEwen, R. Tufts, C. Phillips, B. Clark, M. Ockert-Bell, P. Helfenstein, J. Burns, J. Veverka, R. Sullivan, R. Greeley, R. Pappalardo, J. W. Head III, M. J. S. Belton, T. Denk 1998b. Evolution of Lineaments on Europa: Clues from Galileo Multispectral Imaging Observations. Icarus, 135, 107-126.

Greenberg, R., P.E. Geissler, G. Hoppa, B.R. Tufts, D.D. Durda, R. Pappalardo, J.W. Head, M.H. Carr, and the Galileo Imaging Team. 1997, Tectonic Processes on Europa: Tidal Stresses, Mechanical Response, and Visible Features. Icarus, 135, 64-78.

Greenberg R., and S.J. Weidenschilling, 1984. How fast do Galilean Satellites spin. Icarus , 58, 186-196.

Helfenstein, P., and E.M. Parmentier, 1985. Patterns of Fracture and Tidal Stresses Due to Nonsynchronous Rotation: Implications for Fracturing on Europa. Icarus, 61, 175-184.

Lucchita, B.L., and L.A. Soderblom, 1982. The geology of Europa. in Satellites of Jupiter (D. Morrison, ed.), University of Arizona Press, Tucson, 521-555.

McEwen, A., L. Keszthelyi, P. Geissler, D.P. Simonelli, M.H. Carr, T.V. Johnson, K.P. Klaasen, H.H. Breneman, T.J. Jones, J.M. Kaufman, K.P. Magee, D.A. Senske, M.J.S. Belton, and G. Schubert 1998. Active volcanism on Io as seen by Galileo SSI. Icarus, 135, 181-219.

McEwen, A. 1986. Tidal reorientation and the fracturing of Jupiter's moon Europa. Nature, 321, 49-51.

Morrison, D., and N. D Morrison 1977. Photometry of the Galilean satellites. In Planetary Satellites (J. Burns and D. Morrison, Eds.). Univ. of Arizona Press, Tucson, 363-378.

Shoemaker, E.M., and R.F. Wolfe 1982. Cratering Time Scales for the Galilean Satellites. In Satellites of Jupiter (D. Morrison, Ed.). Univ. of Arizona Press, Tucson, 277-339.

Smith, B.A., L.A. Soderblom, T.V. Johnson, A.P. Ingersoll, S.A. Collins, E.M. Shoemaker, G.E. Hunt, H. Masursky, M.H. Carr, M.E. Davies, A.F. Cook II, J.M. Boyce, G.E. Danielson, T. Owen, C. Sagan, R.F. Beebe, J. Veverka, R.G. Strom, J.F. McCauly, D. Morrison, G.A. Briggs, and V.E. Suomi, 1979. The Galilean satellites and Jupiter: Voyager 2 imaging science results. Science , 206, 927-950.

Thomas, P.C., D. Simonelli, J. Burns, M.E. Davies, A.S. McEwen, M. Belton, and the Galileo SSI Team 1997. Shapes and Topography of Galilean Satellites from Galileo SSI Limb Coordinates. LPSC XXVIII, 1429.